はじめに
まず、小梁の設計をする上で、必要な知識であり、構造設計における基本中の基本「C,M0,Q」について、少し書きたいと思います。
(構造設計者の中では既知の事柄過ぎて、あまり書物には掲載されていないような気がします…)
「 C,M0,Q 」とは??
まず「 C,M0,Q 」とは、以下で示す意味になります。
C:両端固定梁の固定端モーメント (kNm)
M0:単純梁(両端ピン梁)の中央部正曲げモーメント (kNm)
Q:せん断力 (kN)
等分布荷重の場合
梁に等分布荷重が作用している場合は、以下で示す値となります。
(この式は覚えるべし。M0はCの1.5倍と頭に入れておくと計算が楽かと)
$$C=\frac{1}{12}wL^2$$
$$M_0=\frac{1}{8}wL^2$$
$$Q=\frac{1}{2}wL$$
w:等分布荷重 (kN/m)
L:長さ (m)
等分布荷重の場合のC,M0を図示すると以下のようになります。
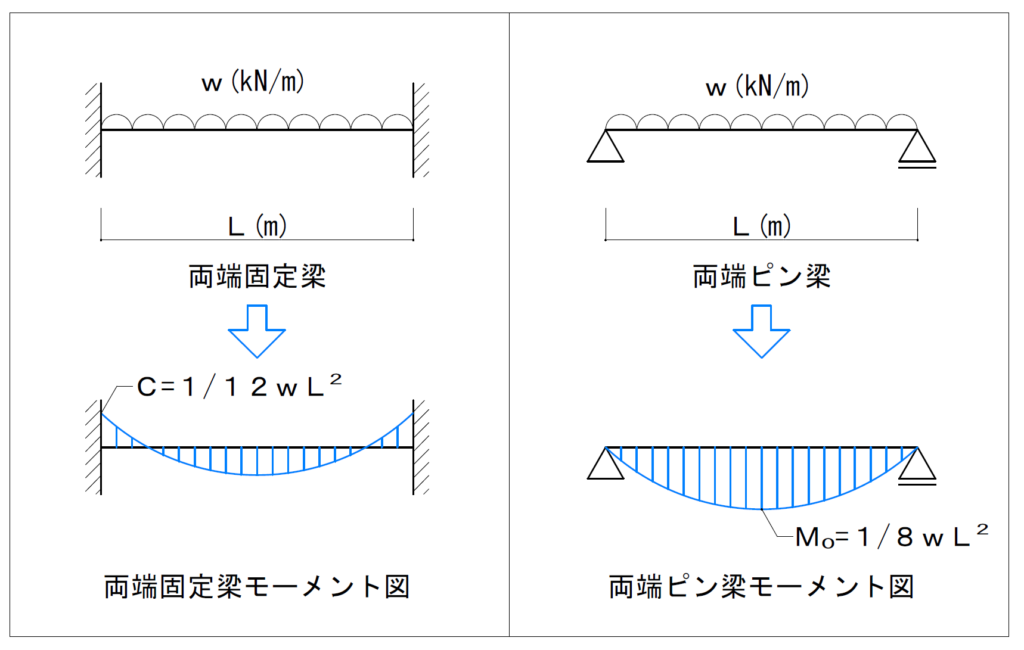
余談ですが、上記の2つのモーメント図、曲線の形状は全く同じです。ただ単に、両端ピン梁の端部の固定度が上がって、グググッと上に持ち上がったのが両端固定梁ってだけなんです。なので、両端固定梁の中央部曲げモーメントは『1/8wL2-1/12wL2=1/24wL2』と公式を暗記せずとも求められます。
この端部が固定されてモーメント図がグググッと持ち上がる感覚、設計者として大事なのかなぁという気がします…
集中荷重の場合
梁の中央に集中荷重が作用している場合は、以下で示す値となります。
(この式も覚えるべし。)
$$C=\frac{1}{8}PL$$
$$M_0=\frac{1}{4}PL$$
$$Q=P$$
P:荷重 (kN)
L:長さ (m)
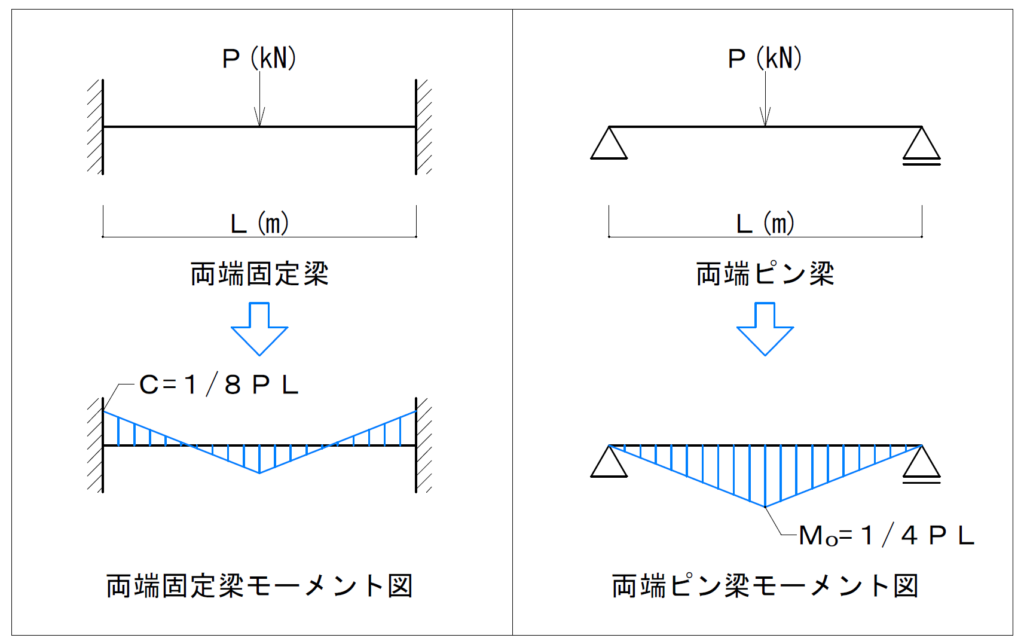
集中荷重の場合のC,M0を図示すると以下のようになります。
等分布荷重と集中荷重が同時に作用する場合
単純に『等分布荷重のC,M0,Q』と『集中荷重のC,M0,Q』を加算すればOKです。
(ただし、正負符号についてはご注意ください。)
$$C=\frac{1}{12}wL^2+ \frac{1}{8}PL $$
$$M_0=\frac{1}{8}wL^2+ \frac{1}{4}PL $$
$$Q=\frac{1}{2}wL+P$$
集中荷重が2個、偏荷重、亀の子、、、等の色々な荷重が生じていても、単純に加算すれば、その梁に生じる『C,M0,Q』が求められます。
次記事では、実際の計算例を示したいと思います。