はじめに
大梁や小梁の設計を行う上で何かと絡んでくる『曲げひび割れモーメントMc』について少し纏めてみようと思います。 大梁や小梁の断面寸法は、この曲げひび割れモーメントMcで決まることが多い気がします。。。
Mcの算定式は、RC規準より以下となります。
Mc(RC規準2010(P73)、(解8.18)式)より引用
σB=18~40(N/mm2)、N/bD=0〜10(N/mm2)の範囲では、柱、梁を通じて曲げひび割れモーメントMcは(解8.18)式で推定される。
$$Mc=0.56\sqrt{σ_B}Z_e+ND/6 (解8.18)$$
Mc:曲げひび割れモーメント(Nmm)
σB:コンクリートの圧縮強度(N/mm2)
Ze:断面係数(mm3)
N,D:軸力(N)、断面せい(mm)
計算例
柱についてはここでは置いておいて、梁について計算してみようと思います。
(梁の曲げひび割れモーメントを算定する場合、梁には軸力が生じていないとし、ND/6=0となります。)
梁の諸条件は『小梁の設計②「計算例」』で用いた断面寸法及び作用曲げモーメントを使い、作用曲げモーメントMが、ひび割れモーメントMc以下であることを確認します。
(作用曲げモーメントMがひび割れモーメントMcを超えると、梁にひび割れが生じるので、長期荷重時にひび割れないように、この確認が必要となります。)
諸条件
小梁寸法:b×D=350×600
コンクリートの圧縮強度:σB=Fc=24(N/mm2)
作用曲げモーメント:M= Mmax=M中央=109.1(kNm)
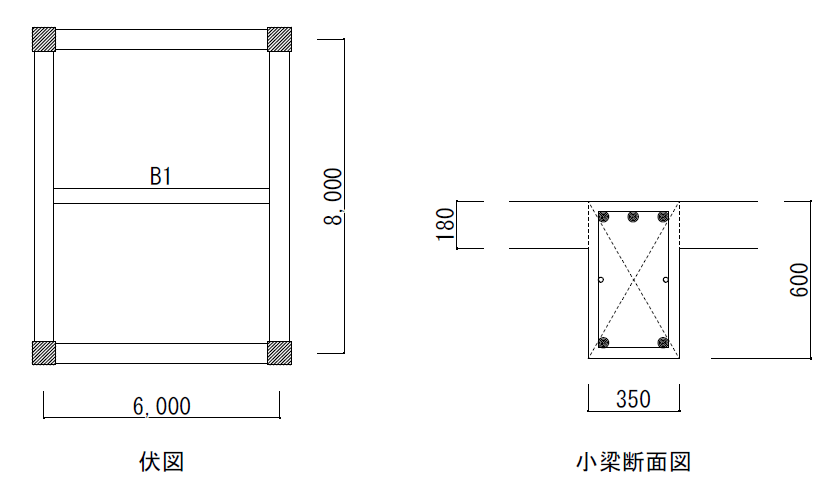
小梁断面のみの曲げひび割れモーメントの算定
まず、断面係数Zeを小梁断面のみで計算してみると、Mcは以下のようになります。
$$Mc=0.56\sqrt{σ_B}Z_e=0.56\sqrt{24}×\frac{350×600^2}{6}$$
=57,611,998(Nmm)=57.6(kNm)
小梁断面のみで考えると、M(=109.1)≧Mc(=57.6)となり、NG…
NGなので、小梁寸法を大きく、、、とはならず、
RC規準によると、梁の剛性評価(Zeの値)は、スラブ付き梁は割り増して計算することとなっています。
断面係数Zeというのは『曲がりにくさ(剛性)』を示す数値で、梁にスラブが付いていたら、曲がりにくそうなのは感覚的に理解出来ると思います。
両側スラブ付きの場合:(梁のみのZ)×2
片側スラブ付きの場合:(梁のみのZ)×1.5
との略算法もありますが、、、ここでは精算法で算定してみます。
なお、ここでは鉄筋の影響は考慮しないこととします。
(鉄筋はコンクリートよりヤング係数が大きく、鉄筋を考慮すると断面係数Zの値は大きくなります。スラブの剛性も考慮して足りなければ、鉄筋も考慮することになります。)
スラブの協力幅
スラブを考慮した場合の断面係数Zeを算定する時、スラブをどこまで含めていいのか、、、がRC規準に記載されています。
RC規準2010(8条,P63)の(8.2)式によると、単純梁の場合は以下のように定められています。
$$ \frac{a}{l_0} <1 の場合 b_a=(0.5-0.3\frac{a}{l_0})a $$
$$ \frac{a}{l_0}≧1の場合 b_a=0.2l_0 $$
a:並列T形断面部材では材の側面から隣の材の側面までの距離
単独T形断面部材ではその片側フランジ幅の2倍
l0:単純梁のスパン長さ
大梁の幅が0.55(m)であるとすると、
a=4.0-0.35/2-0.55/2=3.55(m)、l0=6(m)より、a/ l0 <1であるので、
$$ b_a=(0.5-0.3\frac{a}{l_0})a= (0.5-0.3\frac{3.55}{6.0})3.55$$
=1.14
以上より、スラブの協力幅は1.14(m)となります。
断面係数の増大率φの算定
スラブの協力幅が求められたので、小梁は以下の図に示す断面として断面係数を算定することとします。
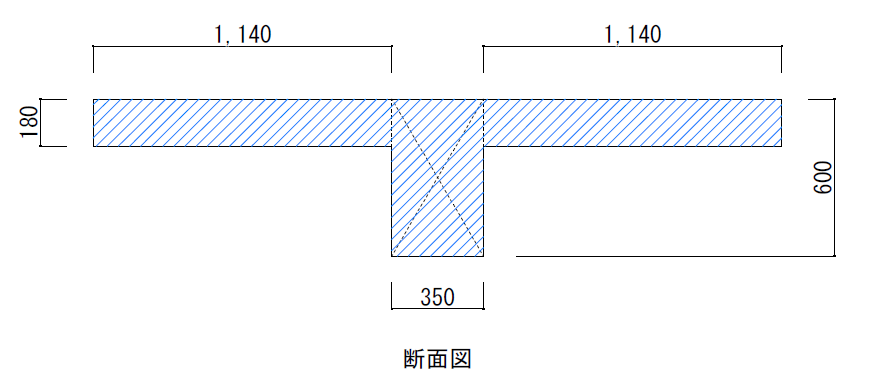
四角形でしたら公式『Z=b×D2/6』で断面係数を算定出来ますが、スラブを考慮する場合は、手計算で断面係数を算出しなければなりません…。
断面係数Zは、図心を通る中立軸に関する断面二次モーメントをIxとし、中立軸から断面最外縁までの距離をyとすると以下の式で求められます。
$$Z=\frac{I_x}{y}$$
まずは、図心Syを算定してみます。
スラブ天端を原点(y=0)であるとすると
$$Sy=\frac{1,140×180×90×2+350×600×300}{1,140×180×2+350×600}$$
=161(mm)
よって、スラブを考慮した断面係数Zは、以下となります。
$$Z=\frac{I_{スラブ}×2+ I_{小梁} }{S_y}= \frac{1,140×180^3/12×2+ 350×600^3/12 }{161} $$
=39,818,683(mm3)
以上よりスラブを考慮した断面係数の増大率φは以下となります。
φ=39,818,683/(350×6002/6)=1.896
スラブを考慮したひび割れモーメントMcの算定
スラブを考慮したひび割れモーメントMcは以下となります。
$$Mc=0.56\sqrt{σ_B}Z_e×φ=0.56\sqrt{24}×\frac{350×600^2}{6}×1.896$$
=109,232,348(Nmm)=109.2(kNm)
スラブを考慮した場合でも、M(=109.1)<Mc(=109.2)となり、ギリギリOK…
きわどいです。。。。
鉄筋を考慮し、作用モーメントMを等分布荷重ではなく亀の子で算定すれば検定値は良くはなりそうです。
が、、、これが実施設計でしたら断面を変更すると思います。。。。
Mcの算定方法の記事なのでご勘弁ください。。。