計算例-1
ここでは、ざっと小梁の断面を算出する例を示したいと思います。
確認申請等もこの程度の検討でも支障がないとは思いますが、あくまでもざっくり検討です。(流れを掴むためには、まずは単純にということで…)
(1) 検討概要
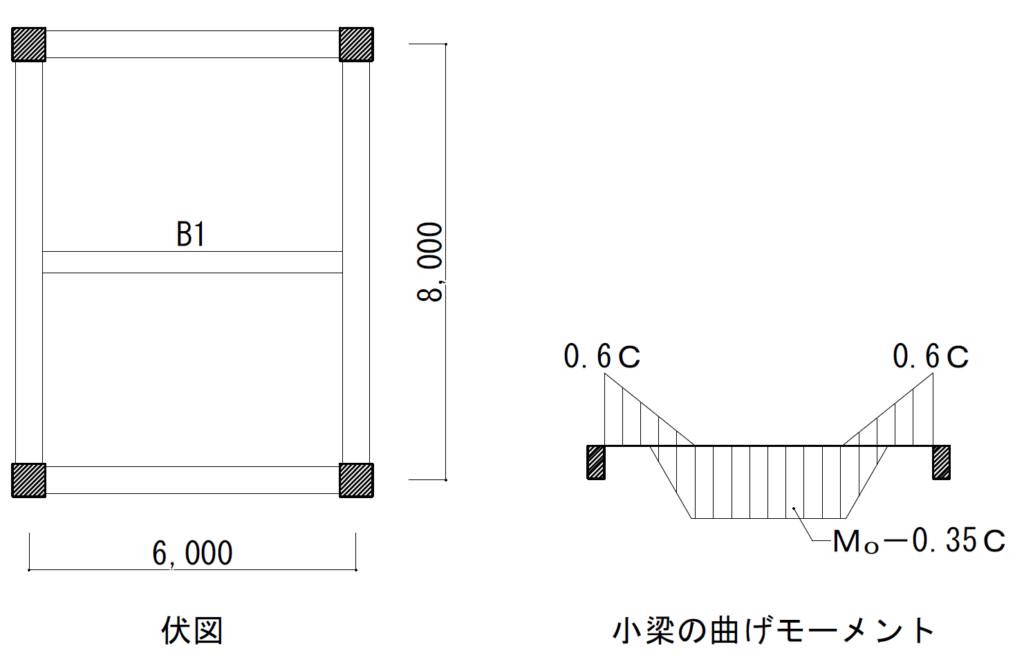
共同住宅のあるスパンにおいて、下図に示すB1梁の主筋及びせん断補強筋の算定をRC規準に準じて行う。大梁に支持された小梁の応力は「RC規準2010(9条,P87),解説図9.3」の単スパン梁の場合で下図のように定める。尚、設計基準強度FcはFc=24(N/mm2)とする。
(2) 仮定荷重
・B1梁は、b×D=350×600(mm)とする。(梁せいはスパンの1/10、幅はノリ)
・スラブはt=180、床仕上げ荷重は600(N/m2)、下階の天井200(N/m2)とする。
・積載荷重は令85条の住宅用の床設計用を用いる。
(小梁はラーメン用を使う場合もあるみたいですが、震動やたわみを考慮して床設計用とします。)
床荷重は以下とする。
固定荷重D.L.=24×180+600+200=5,120 (N/m2)
積載荷重L.L.=1,800 (N/m2)
設計荷重T.L.=5,120+1,800=6,920(N/m2) →7.0(kN/m2)
小梁自重は以下とする。
24×0.35×(0.60-0.18)=3.528 (kN/m) →3.6(kN/m)
(コンクリート単位体積重量(kN/m3)×小梁幅(m)×スラブを抜いた小梁せい(m))
(3) 作用応力の算定
ここでは、床荷重は一様に等分布荷重として小梁に作用しているとする。単位長さあたりの等分布荷重wは以下とし、小梁長さLはL=6.0(m)とする。
w=7.0×8.0/2+3.6=31.6(kN/m)
(w(kN/m)=床荷重(kN/m2)×支配幅(m)+小梁自重(kN/m))
C,M0,Qは以下となる。
$$C=\frac{1}{12}wL^2= \frac{1}{12}31.6×6.0^2=94.8(kNm) $$
$$M_0=\frac{1}{8}wL^2 = \frac{1}{8}31.6×6.0^2=142.2(kNm) $$
$$Q=\frac{1}{2}wL= \frac{1}{2}31.6×6.0=94.8(kN) $$
以上より小梁に作用する応力は 「RC規準2010(9条,P87),解説図9.3」より以下となる。
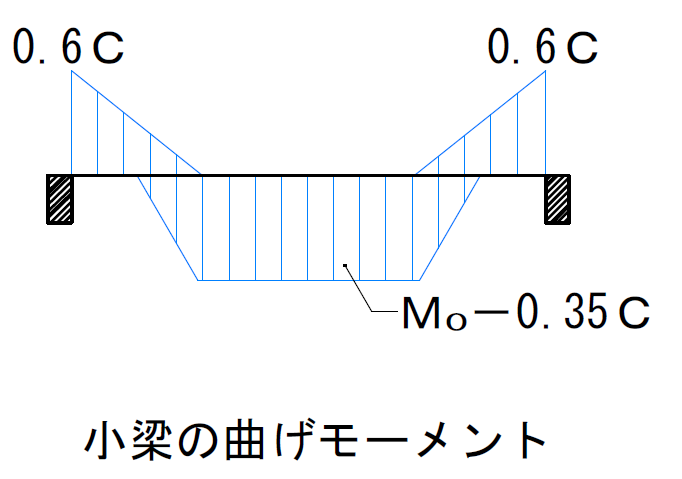
端 部:M端部=0.6C=0.6×94.8=56.88 →56.9(kNm)
中央部:M中央=M0-0.35C=142.2-0.35×94.8=109.02 →109.1(kNm)
せん断:Q=94.8(kN)
(4) 主筋の算定
許容曲げモーメントは、RC規準2010(13条,P121)によると以下となる。
Ma=at・ft・j
Ma:梁の許容曲げモーメント(kNm)
at :引張鉄筋断面積(mm2)
ft :引張鉄筋の許容引張応力度(N/mm2)で、SD295Aの長期は195(N/mm2)
j:梁の応力中心距離(mm)で、7/8d
d:梁の有効せい(mm)で、鉄筋重心位置は小梁面から80mmとする。
以上より、主筋を以下のように算定した。
(右辺のft・jを左辺に持ってくれば必要atが算定できます)
端 部:at= M端部 /(ft×j)=56.9×106/(195×(600-80)×7/8)=641.3(mm2)
→3-D19(=3×287=861(mm2))
中央部: at= M中央 /(ft×j)=109.1×106/(195×(600-80)×7/8)=1,229.6(mm2)
→5-D19(=5×287=1,435(mm2))
(5) あばら筋の算定
RC規準2010(15条,P151)により、作用せん断力Qが(15.1)式により算定される長期許容せん断力 QAL 以下であることを確認する。
また、あばら筋比pwはRC規準2010(15条(4)ⅱ))により0.2%以上とする。
(15.1)式は以下
QAL=b・j・α・fs
$$ただし、α=\frac{4}{\frac{M}{Qd}+1} かつ 1≦α≦2$$
b:梁の幅(mm)
j:梁の応力中心間距離で7/8d(mm)
d:梁の有効せい(mm)
fs:コンクリートの長期許容せん断力(N/mm2)
=Fc/30 かつ (0.49+Fc/100) (Fc≧21は,0.49+Fc/100)
α:梁のせん断スパン比M/Qdによる割増係数
M:設計する梁の長期荷重による最大曲げモーメント(kNm)
Q:設計する梁の長期荷重による最大せん断力(kN)
まず、αを算定する。 Mmax=M中央=109.1(kNm)、 Q=94.8(kN) 、d=0.6-0.08=0.52(m)より
$$α=\frac{4}{\frac{M}{Qd}+1}= \frac{4}{\frac{109.1}{94.8×0.52}+1}=1.244 $$
b=350(mm)、j=(600-80)×7/8(mm)、α=1.244、fs=0.49+24/100=0.73(N/mm2)より
QAL=350×(600-80)×7/8×1.244×0.73=144,618(N)=144.6(kN) ≧Q(=94.8) →OK
あばら筋を2-D10@200とする。
$$p_w= \frac{a_w}{b×x} =\frac{2×71}{350×200}=0.00202 ≧0.2% →OK $$
RC規準には長期許容せん断力が(15.1)式の他に(15.2)式が示されています。ここでは、その違いについて少し触れてみたいと思います。
(15.2)式は以下
QAL=b・j{α・fs+0.5・wft・(pw-0.002)}
b,j,d,fs,α:(15.1)式と同じ
pw:梁のあばら筋比 。
pwの値が0.6%を超える場合は0.6%として許容せん断力を計算する
$$ p_w=\frac{a_w}{bx}$$
aw:1組のあばら筋の断面積(mm2)
b:梁幅(mm)
x:あばら筋の間隔(mm)
(15.1)式と(15.2)式の違いは、b・j・0.5wft (pw-0.002)の有無となります。
(15.2)式をみると以下のように解体できます。
前半の項「α・fs」:コンクリートがせん断力に対して頑張れる値
後半の項「0.5wft (pw-0.002)」:鉄筋がせん断力に対して頑張れる値
つまり、鉄筋のせん断力を期待するか否かの違いとなります。
RC規準には、「長期荷重によるせん断ひび割れを許容する場合には、(15.2)式により算定してもよい」と記載されています。
つまり、コンクリートの許容せん断力を超えて(=ひび割れる)鉄筋にまでせん断力を負担させちゃう場合は、鉄筋のせん断耐力も加えてもまぁいいかなぁ、ということ。
設計者次第ですが、小梁にひび割れを許容してしまうと、震動やたわみが生じて居住者のクレームに繋がるので、通常はひび割れを許容しないこととしています、、、。
基本は、コンクリートでせん断力をカバーして、現場が始まって、どうしても荷重が増えちゃった時には、鉄筋も見ちゃおうか、、、くらいがいいのかなぁと思います。
(6) 算定結果
B1小梁断面は、以下のようになる。
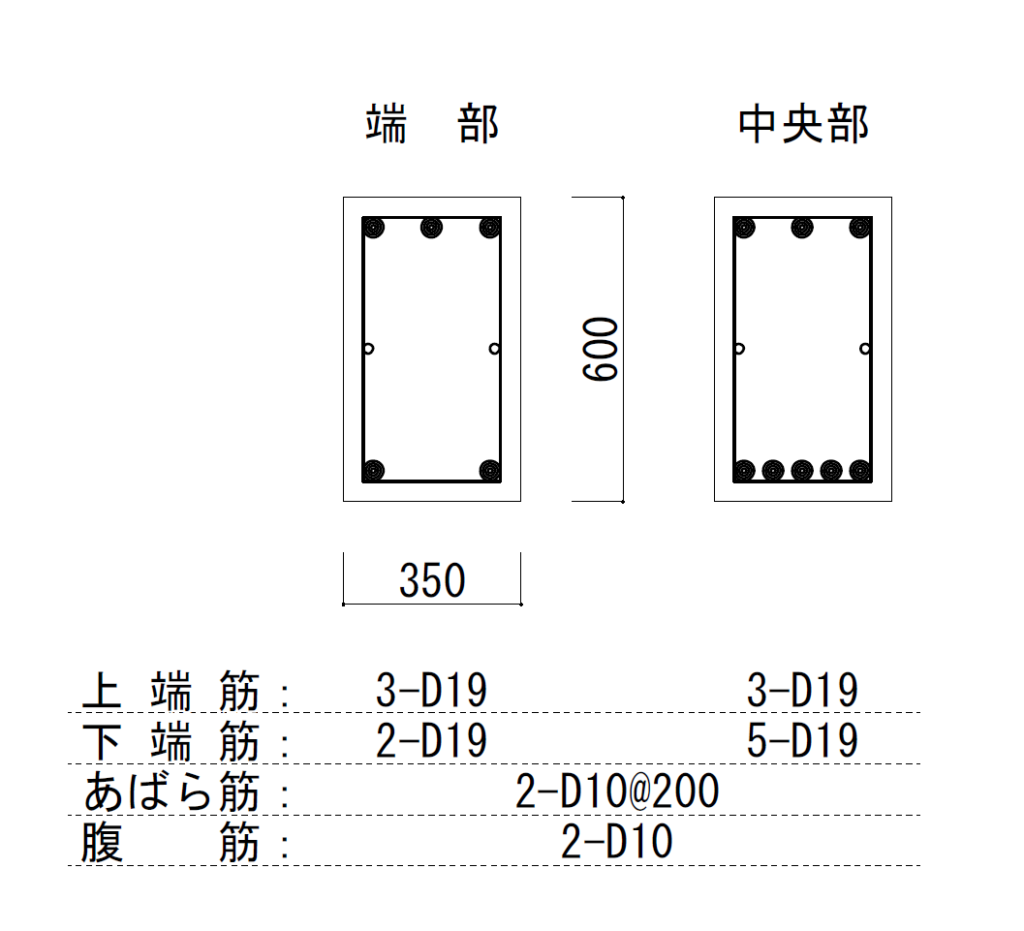
断面寸法は、ひび割れモーメントMcrによって決まることが多いですが、ここでは省略します、、、。
梁幅350mmで5-D19はギリギリ入ります。いざとなったら2段筋にすればいいかなぁと。2段筋にした場合、鉄筋重心位置が変わり、dが少し小さくなりますが、まぁ大丈夫でしょう。
端部上端と中央下端しか、計算上は算定していません。というか、計算上は端部下端と中央部上端は鉄筋はほぼ不要。。。でも、端部下端と中央部上端については、まぁ上下筋の反対側の半分程度以上いれておけばOKです。モーメント図とカットオフ位置を想像して頂ければ分かるかと思います。
亀の子でCM0Qを算定した場合との違いは、おいおいやってみます。そんなに配筋に変更は無いかなぁとは思います。(中央下端が1本くらい減るかも。) どうせ仕上げとかスパンとか設計が進むと変わるでしょうから、、、危険側に変更されても対応できるように、ざっと計算する場合はこれでOKじゃないかなぁと思います。